Noção intuitiva de limite

Para o estudante novato de cálculo, o conceito de limite de uma função é difícil de entender formalmente e, algumas vezes, até uma noção intuitiva é pouca clara.

Uma definição formal de limite de uma função é a seguinte (a definição a seguir foi retirada do livro Calculus: Early Transcedentals, 8ª edição, do James Stewart):

Seja f uma função definida em algum intervalo aberto que contém o número a exceto, possivelmente, pelo próprio número a.

O limite de f(x), à medida que x se aproxima de a, é L se, e somente se, para cada número \epsilon > 0 existir um número \delta > 0 tal que:

0 < |x-a|< \delta \implies |f(x) - L| < \epsilon

O limite é expresso por:

\lim_{x \to a} f(x) = L

Essa é a famosa definição “epsilon-delta” do limite de uma função. Não se preocupe se você não entendeu: muitos estudantes perdem noites e mais noites de sono (e um bocado de cabelo) para entender e aprender a provar que a definição está correta.

Será que é possível entender o conceito de limite sem entrar em mais detalhes matemáticos? Afinal, o que é o limite?

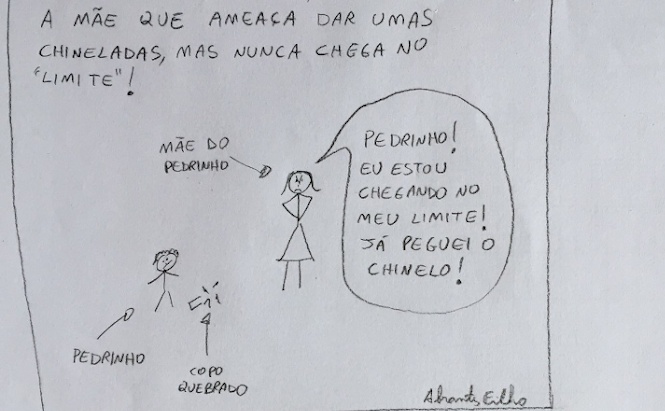
Imagine a seguinte situação: existe um menino muito arteiro, o Pedrinho, que vive quebrando várias coisas em casa.

A cada travessura do Pedrinho sua mãe fica com mais raiva e ameaça: “Pedrinho! Eu estou chegando no meu LIMITE! A próxima coisa que você aprontar vai tomar umas boas chineladas”!

Mas há um problema: por mais travessuras que o Pedrinho apronte, por mais que ele quebre coisas em casa, sua mãe nunca dá umas boas chineladas nele pois seu nível de raiva nunca “chega no limite”.

Eu ilustrei essa situação da seguinte forma:

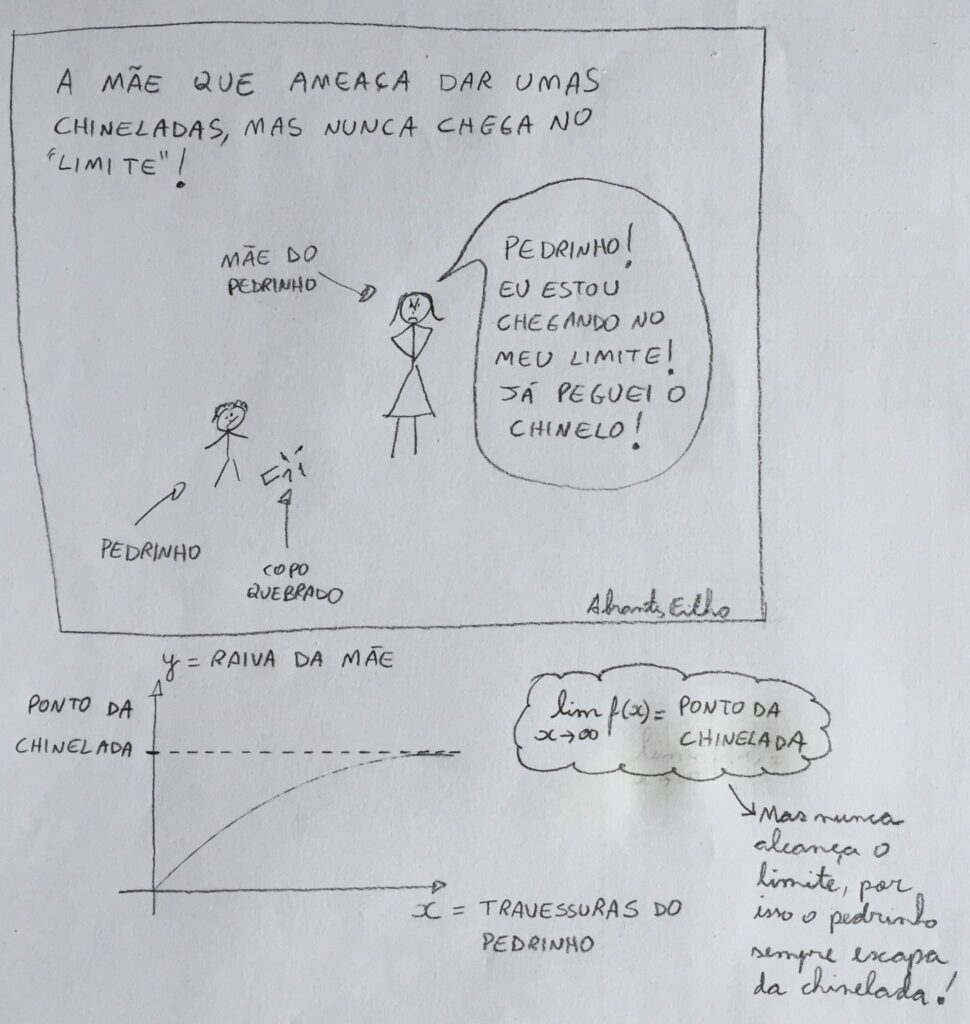
O gráfico acima ilustra a quantidade y de raiva da mãe como uma função f da quantidade x de travessuras do Pedrinho: y = f(x). Note que existe um nível específico de raiva da mãe que dispara as chineladas, o “Ponto da Chinelada”.

Agora repare o seguinte: à medida que as travessuras do Pedrinho aumentam, o nível de raiva da mãe também aumenta mas, na situação ilustrada, nunca chega, nunca alcança, o valor do Ponto de Chinelada, apesar de ficar mais e mais e mais próximo (assim o Pedrinho está, até agora, escapando de umas poucas e boas).

O valor do Ponto da Chinelada é o LIMITE da raiva da mãe quando as travessuras aumentam:

\lim_{\text{travessuras aumentam}} \text{Raiva da Mãe} = \text{Ponto da Chinelada}

Ou, em linguagem mais “matemática” para a situação ilustrada:

\lim_{x \to \infty} f(x) = L = \text{ Ponto da Chinelada}

Note que o LIMITE é o valor que a função TENDE a alcançar (a raiva da mãe TENDE a alcançar o Ponto da Chinelada) mas, não é necessário que o valor da função alcance, de fato, o valor limite.

O que importa é que, à medida que as travessuras aumentam, a raiva da mãe tende a alcançar um valor específico. Esse valor específico L (“Ponto da Chinelada”) é o limite da função nessa situação específica (quando as travessuras do Pedrinho aumentam indefinidamente).

Ah!, sim… o mesmo ocorre com o pai do Pedrinho mas, para ele, qualquer coisa próxima do limite já está bom o suficiente para disparar o Ponto da Chinelada (e por isso o Pedrinho só apronta quando o pai não está em casa)!

Obviamente essa é uma analogia muito simplória e existem inúmeras outras considerações a serem feitas. Mas para uma primeira noção intuitiva do que o limite de uma função é, acredito que seja um bom exemplo.