Régua de cálculo (slide rule): 03 – Que modelo comprar? Onde comprar?

1. Que modelo comprar?

Talvez a maior dúvida para quem está aprendendo a utilizar réguas de cálculo seja a escolha do modelo a ser adquirido.

Se você leu o artigo anterior desta série, Régua de cálculo (slide rule): 02 – Onde aprender?, e visitou os diversos sites e recursos indicados, provavelmente ficou espantado com a enorme quantidade de modelos diferentes, de diversos fabricantes, em diversos tamanhos e formatos, com diferentes escalas e para inúmeras finalidades.

Eu não tenho idéia de quantos modelos diferentes foram fabricados no século XX mas, se eu fosse dar um chute educado, diria mais de mil.

Essa variedade toda intimida quem está começando a estudar o assunto. Eu mesmo demorei quase três semanas até entender as diferenças básicas entre as diversas opções e definir que tipo de régua seria adequada para minhas pretensões.

Partindo de meu objetivo geral, aprender a usar réguas de cálculo para me tornar mais independente de calculadoras e melhorar minha capacidade de estimação e cálculos mentais, resolvi então que:

• Os modelos circulares (e outros mais exóticos) não seriam adequados, pois são mais difíceis de encontrar, mais difíceis para aprender e há pouco material de ensino disponível na internet (quando comparado aos modelos clássicos); e
• Os modelos com finalidades específicas (cálculos para aviação, cálculos balísticos, cálculos elétricos, etc.) não serviriam pois meu interesse é usar as réguas de cálculo como uma calculadora “geral”.

Decidi então me ater aos modelos clássicos mesmo, como a Keuffel & Esser (K&E) 4090 ilustrada abaixo:

Dada a variedade dos modelos eu não fui capaz de classificá-las em esquemas, grupos ou uma taxonomia de acordo com suas diversas características.

O que eu consegui fazer foi identificar as características menos e mais importantes e, a partir daí, escolher os modelos que seriam mais adequados para mim. Apresento a seguir essas características.

1.1. Características menos importantes

Algumas coisas não são tão importantes a ponto de influenciar decisivamente a escolha de um modelo clássico de régua de cálculo. Podem até ter importância secundária, mas não fundamental. São elas:

• Fabricante: eu não encontrei nenhuma crítica severa à construção das réguas de cálculo dos diferentes fabricantes, no máximo algumas queixas pontuais e secundárias, por exemplo: o cursor dos modelos X do fabricante Y é de plástico e não de vidro. Eu ficaria preocupado com algum fabricante se encontrasse críticas dizendo que as escalas estavam erradas ou não alinhadas, mas isso não ocorreu. Então, para mim, o fabricante não é decisivo na hora da escolha.

• Material: as réguas de cálculo foram produzidas em madeira, bambu, diversos tipos de plásticos, alumínio ou outras ligas metálicas, e madeira ou bambu revestido de plástico. Não encontrei nenhuma crítica severa à nenhuma régua devida ao tipo de material utilizado em sua fabricação. Ao contrário: é uma espécie de consenso de que independentemente do material utilizado, se a construção é bem feita, todas funcionam muito bem. Algumas pessoas argumentam que réguas de bambu revestidas por plástico são mais bonitas (ou não) mas esse tipo de coisa não é fundamental na escolha de uma régua (pelo menos para mim… se beleza for fundamental para você, sinta-se à vontade). Uma crítica às réguas de plástico (totalmente plásticas ou de madeira/bambu revestidas de plástico) é que costumam amarelar com o tempo.

• Lupa no cursor: alguns modelos possuem uma lupa ou lente de aumento no cursor da régua, para facilitar a leitura dos números e marcações das escalas. Como tenho 9 graus de miopia em ambos os olhos eu consigo enxergar muito bem de perto e esse tipo de acessório não é fundamental para mim.

• Manual de instruções: alguns modelos são acompanhados de manuais detalhados de uso, outros apenas de um pequeno folheto com informações básicas e, dependendo do fabricante, você pode receber um manual em japonês, alemão ou outra língua. Mas considerando que é possível encontrar com facilidade na internet os manuais adequados, a qualidade do manual de instruções que acompanha a régua também não é fundamental.

• Cores na régua: existe uma padronização, seguida por quase todos os fabricantes, que as escalas inversas (CI, DI, CIF, etc.) são vermelhas e as demais escalas são pretas. Além dessa padronização, alguns fabricantes utilizam outras cores para enfatizar e destacar certas regiões e escalas na régua. Essas regiões coloridas facilitam o uso, sem dúvida, mas não são absolutamente essenciais.

1.2. Características mais importantes

Agora que já sabemos o que não é tão importante em uma régua de cálculo, vamos entender o que realmente faz a diferença. As características abaixo devem ser sua principal preocupação ao escolher qual régua comprar:

• Escalas em um único lado ou nos dois lados: inicialmente as réguas de cálculo só possuíam escalas em um único lado, a “frente” da régua. Nesse tipo de régua o “verso” trazia diversos tipos de informações impressas, por exemplo, tabelas de conversão de medidas, tabelas de conversão de unidades do sistema internacional para o sistema inglês, ou áreas sob a curva normal. Cada fabricante direcionava um determinado modelo para um público específico (engenheiros, estatísticos, etc.) e colocava no verso informações pertinentes a esse público. Com a evolução das réguas os fabricantes passaram a utilizar os dois lados para colocar escalas de cálculo, surgindo assim as réguas chamadas de duplex. A vantagem das réguas duplex é óbvia: utilizando os dois lados a régua pode conter escalas para mais tipos de cálculos. Além disso essas réguas são construídas de forma que você pode começar a fazer um cálculo em um lado, virar a régua, e continuar o cálculo do outro lado com uma outra escala (e repetir esse processo).

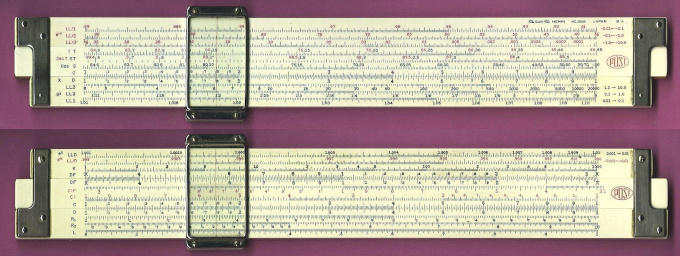
• Tamanho: apesar de algumas variações as réguas de cálculo foram fabricadas em 3 tamanhos padronizados: 5 polegadas, 10 polegadas e 20 polegadas (aproximadamente 13 cm, 25 cm e 50 cm, respectivamente). O tamanho é importante pois quanto maior a régua, mais marcas e gradações as escalas podem ter, aumentando assim a precisão da leitura dos números. As réguas mais utilizadas são, sem dúvida, as de 10 polegadas, pois apresentam um balanço razoável entre tamanho, gradações nas escalas e praticidade. As réguas de 5 polegadas são consideradas réguas de bolso, pois podem ser facilmente carregadas (apesar de gradações menos precisas nas escalas).

• Quantidade e variedade de escalas: esta é a principal característica que você deve observar ao escolher um modelo de régua de cálculo. Os modelos mais simples das réguas com escalas em apenas um lado têm somente 4 ou 5 escalas básicas (para multiplicação e divisão). As duplex mais complexas têm entre 23 a 33 escalas! Em geral, quanto mais escalas uma régua tem, melhor ela é. Isso ocorre pois você pode fazer diferentes tipos de cálculos (trigonométricos, exponenciais, etc.), e pode fazer o mesmo cálculo de modos diferentes, dependendo do problema em questão. Existe uma padronização dos nomes das escalas (C, CI, D, DF, K, B, CIF, LL0, etc.) e as principais são listadas a seguir:
  • C e D: representam f(x) = x. São as escalas fundamentais para os cálculos, e base de comparação para todas as outras escalas.
  • CI e DI: representam f(x) = \cfrac{1}{x}. São as escalas inversas (recíprocas) de C e D, respectivamente.
  • CF e DF: representam f(x) = \pi x. São escalas que começam no valor de pi e usadas para problemas envolvendo essa constante (como círculos e esferas).
  • CIF e DIF: representam f(x) = \cfrac{1}{\pi x}. São escalas inversas (recíprocas) de CF e DF, respectivamente.
  • A e B: representam f(x) = x^2. São escalas utilizadas para calcular o quadrado e a raiz quadrada de um número.
  • K: representa f(x) = x^3. É utilizada para calcular o cubo e a raiz cúbica de um número.
  • L: representa f(x) = \log_{10} x. É utilizada para calcular os valores dos logarítmos (apenas a mantissa) das outras escalas.
  • LL0: representa f(x) = e^{0.001x}. É utilizada para calcular potências maiores ou iguais a 1, mais complicadas que quadrados (A e B) e cubos (K), permitindo calcular potências com base e expoente não inteiros.
  • LL1: representa f(x) = e^{0.01x}. Utilização análoga à da escala LL0.
  • LL2: representa f(x) = e^{0.1x}. Utilização análoga à da escala LL0.
  • LL3: representa f(x) = e^x. Utilização análoga à da escala LL0.
  • LL00: representa f(x) = e^{-0.001x}. É utilizada para calcular potências maiores do que 0 e menores do que 1, mais complicadas que quadrados (A e B) e cubos (K), permitindo calcular potências com base e expoente não inteiros.
  • LL01: representa f(x) = e^{-0.01x}. Utilização análoga à da escala LL00.
  • LL02: representa f(x) = e^{-0.1x}. Utilização análoga à da escala LL00.
  • LL03: representa f(x) = e^{-x}. Utilização análoga à da escala LL00.
  • S: escala dos senos e dos cossenos, medidos em graus. Pode representar 4 coisas diferentes: f(x) = \sin x, f(x) = \cos x, f(x) = \arcsin x e f(x) = \arccos x.
  • T: escala das tangentes e cotangentes, medidas em graus. Pode representar f(x) = \tan x, f(x) = \cot x e f(x) = \arctan x.
  • ST: escala para ângulos pequenos, em radianos; para conversão entre graus e radianos; para cálculo (junto com marcações especiais na escala C) de ângulos em minutos e segundos.
  • P, P1, P2: escalas Pitagóricas, representa f(x) = \sqrt{1-x^2}.
  • Sh, Sh1, Sh2: escalas para o inverso do seno hiperbólico, representam f^{-1}(x) = \cfrac{e^x - e^{-x}}{2}.
  • Ch, Ch1, Ch2: escalas para o inverso do cosseno hiperbólico, representam f^{-1}(x) = \cfrac{e^x + e^{-x}}{2}.
  • Th: escala para o inverso da tangente hiperbólica, representa f^{-1}(x) =\cfrac{e^x - e^{-x}}{e^x + e^{-x}}.
  • Outras: algumas réguas de cálculo acrescentam outras escalas menos comuns e não padronizadas para funções específicas, como por exemplo as escalas CF/M, DF/M, DFM, Lg, Ln, KZ, V, TI1, TI2 e outras.

Como exemplo de uma régua com muitas escalas e extremamente versátil, temos a Aristo Multilog 0970, que é uma régua duplex com 10 polegadas de comprimento e 24 escalas (11 na frente e 13 no verso):

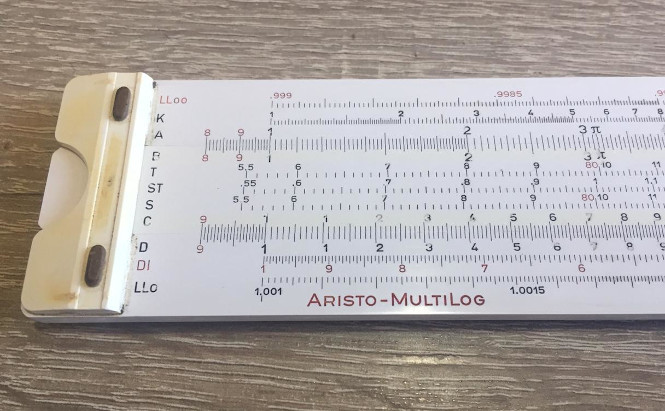
Como exemplo de uma régua com um número menor de escalas, temos a Faber-Castell 67/54b, que é uma régua que só tem escalas na frente, 5 polegadas de comprimento e 13 escalas (7 no corpo, 3 na parte frontal do slide e 3 na parte traseira do slide):

1.3. Resumindo: que modelo comprar?

Uma regra subjetiva, baseada na discussão acima, é a seguinte:

• Se você está querendo uma régua portátil para carregar em sua bolsa ou estojo, procure uma régua de 5 polegadas com o maior número de escalas possível;
• Se você está querendo uma régua para usar como sua calculadora de mesa, procure uma régua duplex de 10 polegadas com o maior número de escalas possível.

2. Onde comprar?

As réguas de cálculo só foram fabricadas até meados da década de 1970, então não há nenhuma loja vendendo réguas novas, recém-fabricadas. Mas como milhares e milhares de réguas foram fabricadas, é fácil encontrá-las em qualquer site de leilão eletrônico, como o Mercado Livre, o OLX ou o eBay.

A regra aqui é ter paciência e visitar periodicamente esses sites para esperar a melhor oferta aparecer. Você encontrará desde réguas absurdamente usadas e em péssimas condições, até réguas nas caixas originais, nunca usadas há décadas, quase como se tivessem saído da fábrica.

Os valores variam muito, de acordo com as condições de conservação das réguas e sua qualidade (duplex, quantidade de escalas, etc.). Você pode encontrar réguas muito boas por cerca de 100 a 200 reais; e também pode encontrar as réguas “top de linha” por qualquer valor entre 400 e 1500 reais (ou até mais!).

Novamente: o segredo é ter paciência! Sempre surgirão réguas boas, inclusive as “top de linha”, por preços camaradas. Por exemplo: eu consegui comprar uma das réguas consideradas “top de linha”, a Faber-Castell 2/83N duplex, com 30 escalas, em perfeito estado de conservação, com caixas e manuais originais por 90 dólares australianos (379 reais), no eBay da Austrália. Claro, ainda tive que pagar o frete de 30 dólares Australianos…

Visite periodicamente esses sites de leiões e espere a melhor oferta!

---

Artigos anteriores desta série:

• Régua de cálculo (slide rule): 01 – Por que aprender?
• Régua de cálculo (slide rule): 02 – Onde aprender?