Prova de que existem infinitos números primos: a demonstração de Euclides e o pensamento matemático na ciência da computação

1 Introdução: pensamento matemático

Uma habilidade fundamental que qualquer estudante de ciência da computação precisa desenvolver é o pensamento matemático, uma maneira de pensar a respeito do mundo que inclui lógica matemática e pensamento analítico bem além das habilidades quantitativas adquiridas no ensino pré-universitário [2, 1].

Aprender a pensar matematicamente não é fácil (pelo menos para mim não está sendo nada fácil). Além das deficiências no aprendizado matemático que se acumularam durante os anos de estudo pré-universitário, o pensamento matemático necessário na ciência da computação é bem diferente: o foco não é mais aprender fórmulas ou macetes para resolver um problema ou uma conta, o foco é pensar em como resolver um problema para o qual você não conhece (ou não existe) uma fórmula pronta [2]. Isso é difícil e leva tempo, muito tempo. Para ilustrar a diferença entre as habilidades quantitativas e o pensamento matemático, considere os dois problemas abaixo:

1. (Apostila Unipró) Próximo ao natal uma fábrica se comprometeu a terminar uma produção com 60 operários em 28 dias. Ao final de 18 dias observou-se que só haviam feito 6/14 da produção. Qual o número de operários que deve ser acrescido aos demais para que a produção acabe no tempo previsto?
2. Prove que o conjunto de números primos é infinito.

Provavelmente você já identificou que o primeiro problema se encaixa no padrão de fórmula de “regra de três composta” e, se ainda se lembra da matemática do ensino médio, conseguirá chegar na resposta correta (devem ser acrescentados 84 operários).

E o segundo problema? Como provar que o conjunto de números primos é infinito? Não existe uma fórmula para isso, nem um padrão de pensamento único que poderia nos levar à resposta. Aliás: o conjunto de números primos é mesmo infinito?

Os dois problemas anteriores ilustram claramente a diferença entre: a) resolver problemas com procedimentos, fórmulas e habilidades quantitativas; e b) conseguir pensar matematicamente com habilidades lógicas e analíticas em problemas para os quais não existe uma fórmula ou procedimento padrão a ser seguido.

Nesse momento já posso ouvir as perguntas dos estudantes novatos: “Isso serve para quê? Onde vou usar isso? Por que eu tenho que estudar isso ao invés de Java?” Bem, para ficar nas duas respostas mais importantes:

• Em primeiro lugar, na área da ciência da computação, o pensamento matemático lhe proporcionará habilidades lógicas e analíticas fundamentais [3, 6] para o entendimento de lógica matemática formal (lógica sentencial e de predicados, provas formais), matemática discreta (provas formais, indução, máquinas de estado, tipos de dados recursivos, teoria dos grafos, redes de comunicação, análise de recorrências), algoritmos (análise da complexidade de algoritmos, prova da corretude de um algoritmo, análise da tratabilidade ou não de problemas por meios algorítmicos), cálculo (entendimento de provas, limites, derivadas e integrais), e muitas outras áreas (álgebra linear, física, teoria da computação, …); e
• Em segundo lugar, e talvez mais importante ainda, o pensamento matemático lhe proporcionará habilidades analíticas básicas para que você aprenda a resolver problemas complexos para os quais ainda não existem soluções prontas, exatamente o tipo de habilidade que empresas e governos buscam [2]: muitas pessoas aplicam fórmulas, poucas tem habilidades anaĺíticas para resolver problemas e adquirir por si mesmas novas habilidades específicas quando necessário.

Se tudo que você busca é desenvolver um Yet Another Software¹ [7, 12], talvez o pensamento matemático não seja tão importante assim mas, se você está em um curso superior de ciência da computação, é um desperdício não aproveitar a chance de aprender uma ferramenta que contribuirá para seu crescimento intelectual, abrirá portas e pavimentará o caminho para aprender coisas de níveis cada vez mais altos, e será utilizado pelo resto de sua carreira.

Por fim, gostaria de apresentar um exemplo clássico do pensamento matemático: a demonstração de Euclides para provar que o conjunto de número primos é infinito. Farei uma breve revisão sobre números primos, na Seção 2, para facilitar o entendimento da prova de Euclides, apresentada na Seção 3.

2 Breve revisão sobre números primos

2.1 O que são números primos?

Os números primos são os números que possuem exatamente dois fatores [13], o próprio número e o número 1. Isso que dizer que os números primos são divisíveis apenas por eles mesmos e por 1. Como ilustração, considere o conjunto A dos números primos menores que 50:

Uma pergunta óbvia que surge é: por que o número 1 não é considerado um número primo? Isso será esclarecido logo, por enquanto apenas saiba que o número 1 não é um número primo, é um número especial, a unidade.

E os outros números como 4, 12, 50? Se eles não são primos, o que eles são? Bem, os outros números são chamados de números compostos, exatamente porque eles são compostos de fatores primos, ou seja, podem ser obtidos através da multiplicação de números primos [14]. Considere a Tabela 1, abaixo, com os números compostos menores que 20 e seus fatores primos:

Agora já está claro que todos os números inteiros positivos podem ser primos, compostos ou a unidade (1).

E mais importante ainda, como ilustrado na Tabela 1, todo número composto pode ser decomposto nos fatores primos que o formam. Mas o que há de especial nisso? A decomposição em fatores primos é única e essa é a chave para o entendimento da demonstração de Euclides.

2.2 A decomposição em fatores primos é única

O fato de que todo número composto pode ser decomposto em fatores primos únicos é conhecido como o teorema fundamental da aritmética [11]. Em inglês costuma-se usar os termos prime factorization ou unique-prime factorization com freqüência.

Mas o que a decomposição em fatores primos únicos quer dizer? Quer dizer que quando um número composto é decomposto em seus fatores primos, a representação é sempre única, exceto pela ordem dos fatores (pois a multiplicação é comutativa). O exemplo abaixo tornará o entendimento mais claro. Considere a decomposição do número 2400 ilustrada na Tabela 2:

A decomposição de 2400 em fatores primos únicos nos diz que, não importa como façamos a decomposição, só existirá uma única maneira de representar 2400: como o produto de cinco números 2, um número 3 e dois números 5, ou seja, como 2⁵ × 3¹ × 5². Nenhum outro número composto existente pode ser representado por esses fatores, portanto a decomposição em números primos é única para todo número composto. Note que a representação da multiplicação de todos os fatores não é única pois, como a multiplicação é comutativa, podemos alterar a ordem de qualquer fator (terceira coluna da Tabela 2) mas os fatores primos continuam sendo únicos.

2.3 Por que o número 1 não é primo?

A decomposição em fatores primos únicos é uma das principais razões pelas quais o número 1 não é um número primo [11]: se ele fosse primo a decomposição em fatores primos não seria única!

Considere a decomposição em fatores do número 6, conforme ilustrado na Tabela 3: se o número 1 fosse primo, não existiria uma única maneira de representar o número 6, portanto o número 1 não é primo.

3 A demonstração de Euclides

Euclides, de Alexandria, o matemátigo grego que dispensa apresentações [9], provou que o conjunto dos números primos é infinito por volta de 300 a.C. [15] e descreveu a demonstração na Proposição 20 do Livro IX de sua obra, Os Elementos [8], da seguinte forma [2, 1]:

1. Suponha que temos o seguinte conjunto de números primos em ordem crescente:
   \{p_1, p_2, p_3, \ldots, p_n\}
   Considere p_1 = 2, p_2 = 3, p_3 = 5, e assim por diante até p_n, o maior número primo conhecido. Como provar que sempre existirá um outro número primo p_i, tal que p_i > p_n, ou seja, como provar que o conjunto de números primos é infinito?
2. Suponha agora que calcularemos o número N da seguinte maneira:
   N = (p_1 \times p_2 \times p_3 \times \ldots \times p_n) + 1
   Obviamente N será muito maior do que todos os números primos utilizados para calculá-lo.
3. Se N for um número primo, já podemos provar que ele é um número primo p_i muito maior do que o último primo conhecido, p_n, então o conjunto pode ser continuado (é infinito).
4. Se N não for um número primo então, pelo teorema fundamental da aritmética, sabemos que ele será dividido por um número primo p_i < N. Mas esse número p_i não será nenhum dos outros primos já conhecidos no conjunto \{p_1, p_2, p_3, \ldots, p_n\} pois, se tentarmos dividir N por qualquer um desses primos já conhecidos, sempre teríamos um resto de 1 (por isso Euclides somou 1 na Equação). Assim, existe um outro número primo p_i > p_n, então o conjunto pode ser continuado (é infinito).

Dois exemplos concretos, a seguir, facilitarão a compreensão da prova de Euclides.

Exemplo 1: Suponha que o conjunto de números primos conhecidos seja o seguinte:

O número N será então:

Ora, 2311 é um número primo maior do que o último primo conhecido no conjunto inicial, 11, então o conjunto pode ser continuado.

Exemplo 2: Suponha agora que o conjunto de números primos conhecido seja o seguinte:

O número N será então:

Ora, 30031 não é um número primo, mas pode ser decomposto nos fatores primos 59 e 509. Encontramos não apenas um, mas dois números primos (59 e 509) maiores do que o último primo conhecido no conjunto inicial, 13, então o conjunto pode ser continuado.

3.1 A demonstração original de Euclides

A demonstração apresentada anteriormente está escrita em linguagem matemática moderna. A título de ilustração, o texto da Proposição 20 do Livro IX de Os Elementos, exatamente como Euclides escreveu, está transcrito abaixo, em inglês. Ele foi retirado da tradução realizada por Sir Thomas L. Heath e publicado no Volume 11 da 1ª edição da coleção Great Books of The Western World (páginas 183–184) [4].

Proposition 20

Prime numbers are more than any assigned multitude of prime numbers.

Let A, B, C be the assigned prime numbers; I say that there are more prime numbers than A, B, C.

For let the least number measured by A, B, C be taken, and let it be DE; let the unit DF be added to DE.

Then EF is either prime or not.

First, let it be prime; then the prime numbers A, B, C, EF have been found which are more than A, B, C.

Next, let EF not be prime; therefore it is measured by some prime number. [VII. 31]

Let it be measured by the prime number G.

I say that G is not the same with any of the numbers A, B, C.

For, if possible, let it be so.

Now A, B, C measure DE; therefore G also will measure DE.

But it also measures EF.

Therefore G, being a number, will measure the remainder, the unit DF: which is absurd.

Therefore G is not the same with any one of the number A, B, C.

And by hypothesis it is prime.

Therefore the prime numbers A, B, C, G have been found which are more than the assigned multitude of A, B, C.

Q.E.D. – Euclides

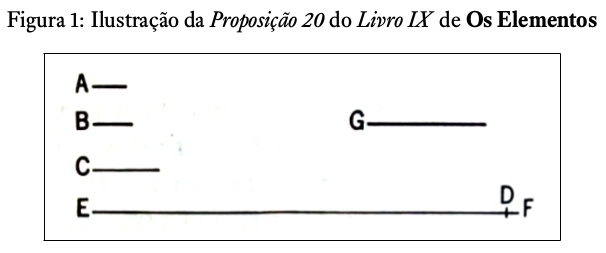
Euclides forneceu um desenho (ver Figura 1) para ilustrar e facilitar o entendimento de sua demonstração. Releia o texto original de Euclides e acompanhe a ilustração tentando “visualizar” o pensamento utilizado pelo grande matemático.

3.2 Euclides, o pensamento matemático, e o estudante de ciência da computação

A demonstração de Euclides é um exemplo simples e clássico do pensamento matemático: como resolver um problema para o qual não existe uma fórmula ou equação?

Euclides utilizou apenas raciocínio lógico e matemático e, sem realizar absolutamente nenhuma conta, provou que o conjunto de números primos é infinito. Esse tipo de pensamento matemático é, em minha opinião, uma habilidade fundamental para os estudantes de ciência da computação.

Não que seja o caso para os estudantes de ciência da computação também se tornarem matemáticos mas, sim, que consigam aprender e desenvolver essa capacidade analítica durante os anos de sua graduação.

4 Conclusão

Meu objetivo neste ensaio foi enfatizar a importância do pensamento matemático para os estudantes de ciência da computação, ilustrando a diferença entre habilidades quantitativas e o pensamento matemático através da demonstração que o conjunto de números primos é infinito, como determinado por Euclides.

Sendo eu mesmo um aluno de um curso de ciência da computação² sinto na pele a dificuldade de aprender e acompanhar várias disciplinas fortemente dependentes do pensamento matemático, como lógica matemática, matemática discreta e complexidade de algoritmos.

Desse modo, mesmo correndo o risco de parecer arrogante³, afinal, sou apenas um aluno, gostaria de concluir com dois pensamentos:

• Aos alunos: aproveitem o tempo da graduação e, além das matérias “legais” e com aplicação imediata, dediquem-se ao estudo das matérias com forte conteúdo matemático e esforcem-se para desenvolver o que aqui foi nomeado como pensamento matemático. O esforço renderá frutos futuros⁴.
• Aos professores e instituições: pelo menos na área específica de ciênca da computação acredito que precisamos de mais, e não de menos, conteúdo matemático (englobando matemática contínua, discreta e concreta). Volta e meia deparo-me com uma leitura ou estudo mais avançado na área de algoritmos, aprendizado de máquina ou inteligência artificial na qual a falta de base matemática causa grande prejuízo à completa e correta compreensão do material. Deixar esse conteúdo em segundo plano ou, até mesmo, postergá-lo para a pós-graduação é privar o aluno da graduação de começar a adquirir uma habilidade analítica fundamental. Entendo a necessidade das instituições de preparar profissionais para o mercado de trabalho (não há nada de errado nisso) mas sacrificar uma habilidade tão importante talvez não seja o melhor caminho.

5 Post scriptum

Acrescentei aqui algumas observações adicionais na tentativa de evitar interpretações equivocadas do que escrevi e de tornar mais claro o foco do texto.

1. Matemática × programação: apesar de acreditar que o estudante de ciência da computação deva desenvolver as habilidades matemáticas tratadas neste texto reconheço, obviamente, que existem analistas de sistemas, programadores e desenvolvedores de software que, mesmo sem tal ampla base matemática, são excelentes em seu trabalho. Crianças e adolescentes utilizando ferramentas online como o Scratch⁵ e o MIT App Inventor⁶ conseguem criar sistemas e aplicativos incríveis. Não é preciso ser excelente em matemática para ser um bom programador: é necessário saber usar uma linguagem de programação e suas ferramentas para resolver um problema. As habilidades matemáticas ajudam, claro, mas não são suficientes nem o principal fator para o sucesso de um programador.
2. Pensamento matemático × pensamento computacional: é importante distinguir aqui o pensamento matemático do pensamento computacional. O pensamento computacional⁷ é mais abrangente, é a capacidade de compreender um problema complexo e desenvolver uma solução que possa ser seguida e implementada por um humano, um computador ou ambos. O pensamento computacional costuma ser dividido em 4 habilidades básicas:
   • Decomposição: capacidade de quebrar um grande e complexo problema em partes menores, mais gerenciáveis e tratáveis;
   • Reconhecimento de padrões: capacidade de, dados os problemas, reconhecer padrões e similaridades entre eles e entre problemas anteriores já resolvidos para facilitar a busca de soluções;
   • Abstração: capacidade de manter o foco somente nas partes importantes do problema, abstraindo detalhes irrelevantes; e
   • Algoritmos: capacidade de desenvolver uma solução passo a passo para o problema.
     
     Nesse sentido o pensamento computacional é muito mais importante para um programador do que o pensamento matemático “puro”. E, de certa forma, toda pessoa utiliza o pensamento computacional ao resolver um problema, por exemplo: um agricultor certamente utiliza uma forma de pensamento computacional ao resolver um problema em sua lavoura, mesmo sem base matemática. Mas, para o cientista da computação, meu entendimento atual é o de que o pensamento matemático proporciona uma base a partir do qual ele pode aplicar diversas e mais avançadas técnicas enquanto resolve um problema.
3. Mais matemática × mais prática: uma discussão que pode surgir a partir da defesa do pensamento matemático na ciência na computação é a seguinte: as instituições de ensino e professores de ciência da computação devem focar em mais matemática ou em mais prática para os alunos (no intuito de melhor prepará-los para o mercado)? Eu, como aluno, não tenho a resposta para isso e minha visão (com um forte viés teórico, reconheço) é apenas isso: minha própria visão. E, claro, pode não ser generalizável ou adequada em todos os contextos e situações. De todo modo, meu entendimento atual é o de que o aluno de ciência da computação precisa de forte conteúdo matemático pois o objetivo é formar um cientista da computação, não apenas mais um programador. Muitos cientistas da computação trabalharão e serão extremamente produtivos como programadores, e não há nada de errado nisso. Mas acredito que o curso de graduação em ciência da computação deve proporcionar ampla base matemática para que o estudante entenda a anatomia e a fisiologia de seu ofício, bem como seja capaz de entender avanços em campos diversos como inteligência artificial e aprendizado de máquina.
4. Matemática × computação: uma interpretação equivocada que pode surgir deste texto é a de que estou dando mais importância à matemática do que às diciplinas “próprias” da computação, como algoritmos, estruturas de dados, teoria da computação e outras. Apesar do foco ser matemático não quero, de modo algum, ignorar ou diminuir a importância das outras disciplinas da área.
   

Referências

[1] Keith Devlin. Sets, Functions, and Logic. Chapman & Hall/CRC, 3 edition, 2003. ISBN 9781584884491. URL https://www.amzn.com/1584884495/.

[2] Keith Devlin. Introductioin to Mathematical Thinking. Keith Devlin, Palo Alto, CA, USA, 1 edition, 2012. ISBN 9780615653631. URL https://www.amzn.com/0615653634/.

[3] Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Matematica Concreta: fundamentos para a ciência da computação. Editora LTC, Rio de Janeiro, 2 edition, 1995. ISBN 9788521610403. URL https://www.amzn.com/dp/0201558025.

[4] Robert Maynard Hutchins. Great Books of the Western World. Encyclopaedia Britannica, Chicago, 1 edition, 1952. URL https://en.wikipedia.org/w/index.php?title=Great_Books_of_the_Western_World&oldid=948034751.

[5] Donald E. Knuth. The Art of Computer Programming, Volumes 1-4. Addison Wesley,ISBN 9780321751041. URL https://www.amzn.com/0321751043.

[6] Eric Lehman, F. Thomson Leighton, and Albert R. Meyer. Mathematics for Computer Science. MIT, 2018 edition, 2018. URL https://courses.csail.mit.edu/6.042/spring18/.

[7] Eric S. Raymond. The on-line hacker Jargon File, version 4.4.7, 2003. URL http://catb.org/jargon/html/index.html. [Online; acesso em
2020/04/20].

[8] Wikipedia contributors. Euclid’s Elements. Wikipedia, The Free Encyclopedia, 2020. URL https://en.wikipedia.org/w/index.php?title=Euclid’s_Elements&oldid=946948825. [Online; acesso em 2020/04/20].

[9] Wikipedia contributors. Euclid. Wikipedia, The Free Encyclopedia,
2020. URL https://en.wikipedia.org/w/index.php?title=Euclid&oldid=943833243. [Online; acesso em 2020/04/20].

[10] Wikipedia contributors. The Art of Computer Programming. Wikipedia, The Free Encyclopedia, 2020. URL https://en.wikipedia.org/w/index.php?title=The_Art_of_Computer_Programming&oldid=946105474. [Online; acesso em 2020/04/20].

[11] Wikipedia contributors. Fundamental theorem of arithmetic. Wikipedia, The Free Encyclopedia, 2020. URL https://en.wikipedia.org/w/index.php?title=Fundamental_theorem_of_arithmetic&oldid=950568548 [Online; acesso em 2020/04/20].

[12] Wikipedia contributors. Yet another. Wikipedia, The Free Encyclope dia, 2020. URL https://en.wikipedia.org/w/index.php?title=
Yet_another&oldid=950801463. [Online; acesso em 2020/04/20].

[13] Wikipedia contributors. Prime number. Wikipedia, The Free Encyclopedia, 2020. URL https://en.wikipedia.org/w/index.php?title=
Prime_number&oldid=951243553. [Online; acesso em 2020/04/20].

[14] Wikipedia contributors. Composite number. Wikipedia, The Free Encyclopedia, 2020. URL https://en.wikipedia.org/w/index.php?title=Composite_number&oldid=951396976. [Online; acesso em 2020/04/20].

[15] Wikipedia contributors. Euclid’s theorem. Wikipedia, The Free Encyclopedia, 2020. URL https://en.wikipedia.org/w/index.php?title=Euclid’s_theorem&oldid=951737760. [Online; acesso em 2020/04/20].

Notas de rodapé

1. Yet Another, abreviado YA ou Ya, costuma ser um qualificador utilizado no nome de programas de computador que são, confessa e explícitamente, não originais. Ver Eric S. Raymond (The on-line hacker Jargon File) ou Wikipedia (Yet Another) para maiores informações.
2. Apesar de atualmente estar no 5º período do curso de ciência da computação, me considero um estudante diferenciado pelos seguintes motivos: a) esta é minha segunda graduação (minha primeira graduação foi em medicina, concluída em 1999); b) tenho mestrado na área de epidemiologia e métodos quantitativos em saúde, concluído e 2002; e c) por preferência pessoal gosto da área de análise de dados, apesar de munca ter sido um aluno muito bom em matemática. Acredito, portanto, não me encaixar bem no esteriótipo do típico estudante de ciência da computação, com seus vinte e poucos anos querendo apenas se formar o mais rápido possível e conseguir entrar no mercado de trabalho. Isso me dá a possibilidade de aprofundar os estudos e apreciar de forma mais profunda as questões teóricas geralmente relegadas a segundo plano pelos estudantes.
3. Ou de estar completamente errado!
4. Acreditem: é frustrante pegar um livro mais avançado para estudar, como o The Art of Computer Program , de Donald E. Knuth, e não conseguir fazer progresso pela falta de compreensão matemática dos algoritmos. Ver: https://cs.stanford.edu/~knuth/taocp.html
5. https://scratch.mit.edu/
6. https://appinventor.mit.edu/
7. Uma das mais simples e interessantes explicações sobre o que é pensamento computacional está no site Bitesize: Computer Science, da BBC: https://www.bbc.co.uk/bitesize/topics/z7tp34j. Vale a pena visitar e ler esse conteúdo!

---

Versões em PDF deste texto:

• PDF para impressão (links ocultos e não coloridos)
• PDF para web (links destacados e coloridos)